Factors terrify me. I can avoid dealing with them most of the time, but they’re immensely useful in a regression when you have a categorical variable with many levels (e.g. “Very Bad”, “Bad”, “Good”, “Very Good”). A common example in economics is when you have a difference-in-differences design and you want to estimate how the treatment effect changes over time, before and after the treatment period.

Here’s a toy example:

library(tidyverse)
library(magrittr)
library(hrbrthemes)

theme_set(theme_ipsum(base_size = 18, axis_title_size = 16))
theme_update(axis.text = element_text(size = 16))

df = 
  data_frame(treated = c(rep(T, 30), rep(F, 30)), 
             id = rep(1:2, each = 30),
             year = rep(2001:2003, 20))

idfe = data_frame(id = 1:2, idfe = c(0.5, 0))
timefe = data_frame(year = 2001:2003, timefe = c(0.25, 0.5, 0.75))

effect = 0.5

df %<>% 
  left_join(idfe, by = "id") %>% 
  left_join(timefe, by = "year") %>% 
  mutate(y = idfe + timefe + if_else(year == 2003 & treated, effect, 0))
  

df %>% 
  group_by(year, treated) %>% 
  summarise(y = mean(y)) %>% 
  ungroup() %>%
  ggplot(aes(x = year, y = y, colour = !treated, linetype = !treated)) + 
  geom_line(size = 1.2) + 
  geom_vline(xintercept = 2002, linetype = 2) + 
  labs(colour = "Treated", linetype = "Treated") + 
  # scale_colour_manual(labels = c("Treated", "Control"), values = c("#bb1200", "#8078bc")) +
  scale_colour_manual(labels = c("Treated", "Control"), values = c("#ea5f94", "#9d02d7")) +
  scale_linetype_manual(labels = c("Treated", "Control"), values = c(1, 2))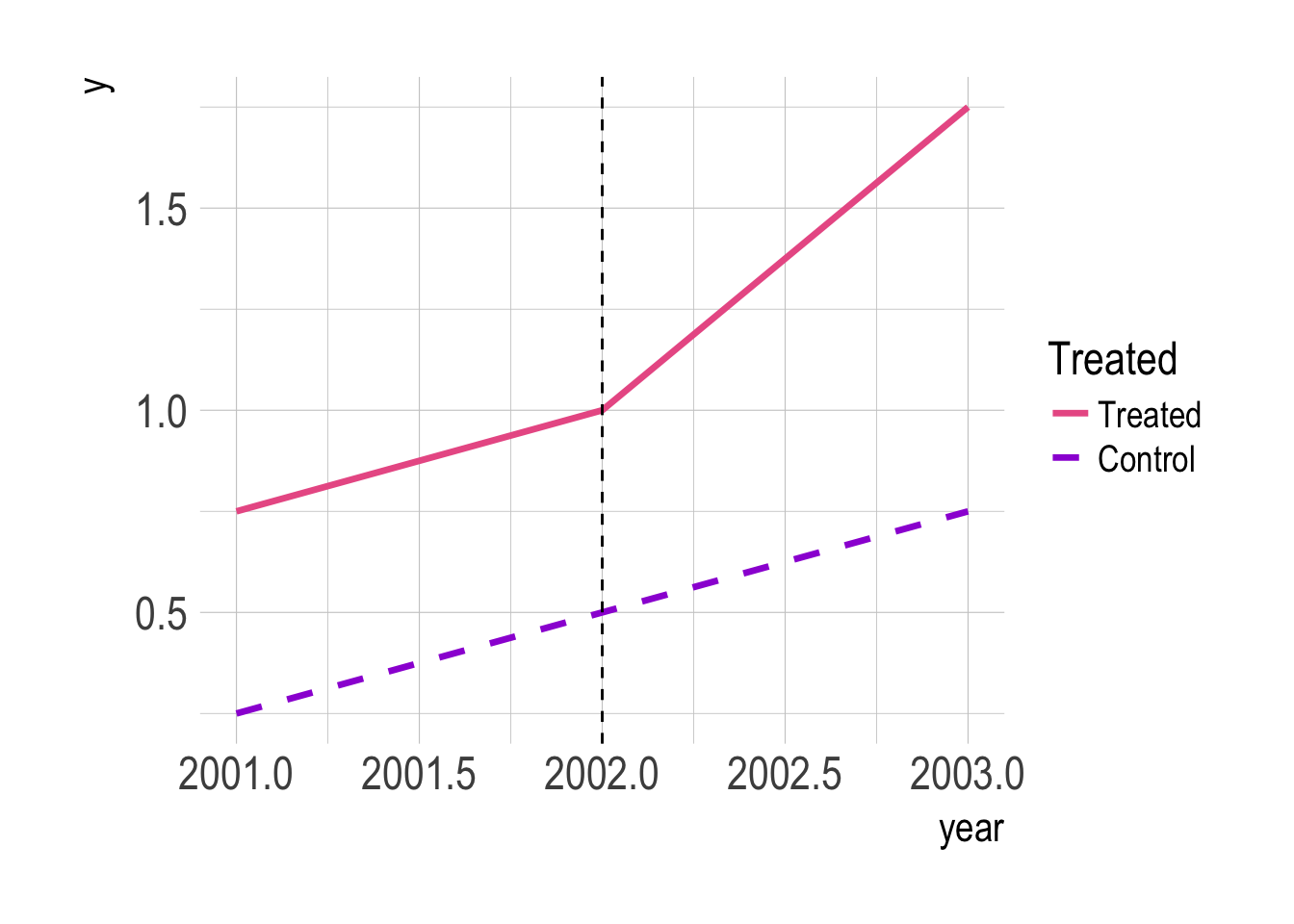

Normally what we want to do here is estimate a separate “treatment” coefficient for the year before treatment and the year after treatment after including person and year fixed effects. Another way of putting it is that we want to estimate the interaction of the treatment variable and the year variable. Since there are 3 years and the treatment is binary, that results in a factor with 6 levels (2001-treated, 2001-control, 2002-treated, …), but only 2 levels are identified. In this example, the pre-treatment coefficient is 0 and the post-treatment coefficient is 0.5.

Normally, we can specify an interaction in the R regression formula with a colon : (e.g. factor(year):factor(treated)), but to help with clarity I’m going to explicitly create the treatment:time interaction variable and call it treat_time.

library(lfe)
library(broom)

df %<>% 
  unite(treat_time, year, treated, remove = FALSE) 
  
felm(y ~ factor(treat_time) | year + id, data = df)

## Warning in chol.default(mat, pivot = TRUE, tol = tol): the matrix is either
## rank-deficient or indefinite

##  factor(treat_time)2001_TRUE factor(treat_time)2002_FALSE 
##                          NaN                          0.0 
##  factor(treat_time)2002_TRUE factor(treat_time)2003_FALSE 
##                          NaN                         -0.5 
##  factor(treat_time)2003_TRUE 
##                          NaN

2 problems:

1. The estimation has returned two coefficients (“2002_FALSE” and “2003_FALSE”), which is the right number of coefficients, but those aren’t the coefficients we wanted (technically we could back out the coefficients since everything is relative but that’s unnecessarily confusing).

2. We have a warning: the matrix is rank-deficient or indefinite. This usually means that the model is collinear and therefore some of the coefficients aren’t identified (hence the NaN coefficients). Even though we expected this, I’d much prefer to not have warning messages pop up in my code. First, if I have to revisit this code at some point in the future, I might not remember why the warning is coming up and have to waste time figuring it out again. Second, if I fix the code and warnings still come up, then I’ll have discovered an error that I would have otherwise overlooked.

Another thing to notice is that one level of the factor has already been left out. What we want to do now is tell R to leave out all the other levels of the factor that we know can’t be estimated instead of returning NaN for a coefficient.

Here’s the solution I came up with:

1. Give the levels of treat_time that we want to leave out the same name. In this example, I’ll just give all those levels the name “FALSE”.

2. Set the levels of the newly defined treat_time using the fct_relevel function from the forcats package so that “FALSE” is the lowest level. This will get R to leave it out in the estimation.

There are 2 ways to perform step 1: make the changes to treat_time as a string, then convert it to factor, or convert it to a factor before making the changes with forcats functions.

# as a string first

df %<>%  
  mutate(treat_time_a = if_else(str_detect(treat_time, "FALSE|2002_TRUE"), "FALSE", treat_time), 
         treat_time_a = factor(treat_time_a), 
         treat_time_a = fct_relevel(treat_time_a, "FALSE")) # set "FALSE" to lowest level

Or:

ctrl_lvl = function(x){
    if_else(str_detect(x, "FALSE|2002_TRUE"), "FALSE", x)
  }

df %<>% 
  mutate(treat_time_b = as_factor(treat_time), 
         treat_time_b = fct_relabel(treat_time_b, ctrl_lvl), 
         treat_time_b = fct_relevel(treat_time_b, "FALSE")) # set "FALSE" to lowest level

knitr::kable(list(df %>% count(treat_time), df %>% count(treat_time_a), df %>% count(treat_time_b)))

The relabelled factor treat_time_a or treat_time_b now has 3 levels rather than 6. If we run the same regression:

felm(y ~ treat_time_a | year + id, data = df)

## treat_time_a2001_TRUE treat_time_a2003_TRUE 
##             -3.04e-17              5.00e-01

No more warning message! And the exact coefficients we wanted!

df %<>% mutate(pretreatment = year == 2001 & treated,
               posttreatment = year == 2003 & treated)

felm(y ~ pretreatment + posttreatment | year + id, data = df)

##  pretreatmentTRUE posttreatmentTRUE 
##         -3.04e-17          5.00e-01